9.1. Vektorräume und Vektoren

- - - - - Diese Seite braucht webEQ! Klicken Sie auf das Logo. - - - - -

9.1. Vektorräume und Vektoren

Zu Beginn dieses Kapitels betrachten wir den R² unter einem neuen Gesichtspunkt. Dabei ist es zweckmäßig, das "alte" Modell - die Elemente des R² sind die Punkte der Zeichenebene - durch ein anderes zu ersetzen: Jetzt stellen wir uns unter einem Element (x, y) Î R ² einen Pfeil vor, der im Koordinatenursprung (0,0) beginnt und mit seiner Spitze im Punkt (x, y) endet. Das Zahlenpaar (4,2) hat also im neuen Modell die folgende Gestalt:

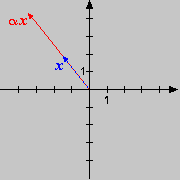
Einerseits betont die Pfeildarstellung geometrische Verhältnisse - so wird z.B. der Nullabstand eines Punktes als Länge des zugehörigen Pfeils sichtbar - andererseits lassen sich Manipulationen der Punkte in der Pfeildarstellung besonders gut nachvollziehen. In dem folgenden Applet etwa kann man per Schieber die Pfeillänge verändern; man achte dabei auf die Änderungen in den Koordinatenwerten:

Ein weiteres Applet stellt das durch zwei Pfeile erzeugte Parallelogramm zusammen mit der Hauptdiagonalen dar ("Parallelogrammgesetz der Kräfte"). Ändert man einen der Pfeile (durch Ziehen der Spitze) so stellt sich die Diagonale neu ein; sie läßt sich also als ein Ergebnis der beiden Ausgangspfeile deuten.

Die in den Applets beobachtbaren Verhältnisse weisen den Weg zu einer Rechenstruktur des R ²: Es wird eine sinnvolle Möglichkeit geben

Zwei Zahlenpaaren des R ² ein drittes Zahlenpaar als Ergebnis zuzuweisen.
Ein Zahlenpaar und einen reellen "Längenfaktor" zu einem neuen Paar zusammenzurechen.

Dieses Vorhaben setzen wir mit der Einführung des Begriffs Vektorraum zunächst in allgemeiner Form um. In einem ersten Beispiel wird dann der R ⁿ, und damit auch der R ², konkret mit der oben angedeuteten Rechenstruktur versehen.

Definition: Es sei V eine Menge auf der zwei Rechenoperationen

+ : V ´ V ® V
· : R ´ V ® V

erklärt sind.

Das Tripel (V, + , · ) heißt eine (reeller) Vektorraum (bzw. ein linearer Raum), falls die folgenden Regeln (Axiome) erfüllt sind:

    (V1)      + ist assoziativ

    (V2)      + ist kommutativ

    (V3)      Es gibt ein neutrales Element 0 Î V mit   0 + v = v = v + 0   für alle v Î V.

    (V4)      Zu jedem v Î V gibt es ein inverses Element -v Î V mit v + (-v) = 0 = (-v) + v.

    (V5)      1·v = v für alle v Î V.

    (V6)      a·(b·v) = (ab)·v für alle v Î V und a,b Î R .

    (V7)      a·(v + w) = (a·v) + (a·w) für alle v,w Î V und a Î R .

    (V8)      (a + b)·v = (a·v) + (b·v) für alle v Î V und a,b Î R .

Die Elemente von V nennen wir Vektoren und die Rechenoperation + die Vektoraddition (auf V); die reellen Zahlen heißen in diesem Zusammenhang Skalare, die Rechenoperation · die skalare Multiplikation (auf V).

Beachte:

Bei der Formulierung der Vektorraumaxiome haben wir für die Summe zweier Vektoren bereits die übliche Schreibweise, v + w statt +(v,w), verwandt. Ebenso für das Vielfache eines Vektors: a·v an Stelle von ·(a,v).
Bei einem skalaren Produkt a·v ist der skalare Faktor grundsätzlich links zu notieren; einen Ausdruck der Form v·a gibt es nicht!
Für a ¹ 0 allerdings setzen wir als Abkürzung fest: $\frac{v}{α} : = \frac{1}{α} v$ .
Als Differenz zweier Vektoren v und w bezeichnen wir den Vektor v - w := v + (-w).
- nennen wir die Vektorsubtraktion. Dabei gilt offenbar: w + (v - w) = v.
Wir vereinbaren, wie üblich, "+ bindet stärker als ·" und lassen (später) das Multiplikationssymbol meist weg.
(V7) z.B. läßt sich damit etwas kürzer formulieren: a(v + w) = av + aw.
Die Bedingungen (V1) bis (V4) lassen sich zusammenfassen zu der Forderung

(V, + , · ) ist eine abelsche Gruppe.

Alle Eigenschaften von abelschen Gruppen sind somit für einen Vektorraum bereits gegeben! Dies sind die hier wichtigsten:
1. Es gibt genau ein neutrales Element in V.
2. Zu jedem v Î V gibt es genau ein inverses Element.
  -v durfte also als Bezeichnung für das inverse Element zu v gewählt werden!
3. -0 = 0
4. -(-v) = v
5. -(v + w) = (-v) + (-w)
Der Beweis ist leicht zu führen.
Die Bedingung (V5) ist eine sog. Normierungsbedingung.
(V6) darf nicht mit einem Assoziativgesetz verwechselt werden, denn die Produkte ab und b·v gehören zu unterschiedlichen Multiplikationen!
(V7) und (V8) dagegen sind echte Distributivgesetze.
In vielen Situationen besteht über die Vektoraddition und skalare Multiplikation kein Zweifel; wir werden dann den Vektorraum (V, + , · ) lediglich durch das Symbol V angeben.
Die Bezeichnung reeller Vektorraum bezieht sich auf die Wahl von R als Skalarenbereich. Ersetzt man diesen Bereich durch einen beliebigen Körper K, so nennt man V einen Vektorraum über K. Auf diesen verallgemeinerten Vektorraumbegriff gehen wir nicht ein. Je nach Güte des Körpers K hat V unterschiedliche Eigenschaften; nicht alle im folgenden notierten Ergebnisse lassen sich daher auf den verallgemeinerten Fall übertragen.

Mit dem Eingangsbeispiel ist i.w. bereits eine ganze Gruppe von gleichartigen Vektorräumen gegeben, und zwar sind dies die Räume R , R², R ³, ... . Wir notieren ihre Elemente von jetzt an im Fettdruck: x, y,... und wählen für die Koordinatendarstellung die traditionelle, senkrechte Form: $x = (\begin{matrix} x_{1} \\ ⋮ \\ x_{n} \end{matrix})$ . Üblich sind auch andere Darstellungen, etwa die Verwendung von Pfeilornamenten ( $\vec{x}, \vec{y},$ ... ) oder Frakturbuchstaben ( $𝔵, 𝔶,$ ... ).

Zentrales Beispiel (1): Es sei n Î N. Setzt man für $x = (\begin{matrix} x_{1} \\ ⋮ \\ x_{n} \end{matrix})$ , $y = (\begin{matrix} y_{1} \\ ⋮ \\ y_{n} \end{matrix})$ Î R ⁿ und a Î R :

$x + y : = (\begin{matrix} x_{1} + y_{1} \\ ⋮ \\ x_{n} + y_{n} \end{matrix})$
           (Koordinatenweises Addieren)

$α ċ x : = (\begin{matrix} α ċ x_{1} \\ ⋮ \\ α ċ x_{n} \end{matrix})$            (Koordinatenweises Multiplizieren)

so ist (R ⁿ, + , · ) ein Vektorraum.
Dabei ist

$0 : = (\begin{matrix} 0 \\ ⋮ \\ 0 \end{matrix})$ der Nullvektor.

$- x : = (\begin{matrix} - x_{1} \\ ⋮ \\ - x_{n} \end{matrix})$ der zu x inverse Vektor (Koordinatenweiser Vorzeichenwechsel).

$x - y = (\begin{matrix} x_{1} - y_{1} \\ ⋮ \\ x_{n} - y_{n} \end{matrix})$ (Koordinatenweises Subtrahieren).

Beweis: Es sind die Vektorraumaxiome (V1) bis (V8) nachzuweisen, eine einfache, aber langwierige Aufgabe. Entscheidend sind dabei die Rechengesetze in R .
(V1): Mit dem Assoziativgesetz für + in R erhält man:

$(x + y) + z = (\begin{matrix} (x_{1} + y_{1}) + z_{1} \\ ⋮ \\ (x_{n} + y_{n}) + z_{n} \end{matrix}) = (\begin{matrix} y_{1} + (x_{1} + z_{1}) \\ ⋮ \\ y_{n} + (x_{n} + z_{n}) \end{matrix}) = x + (y + z)$ .

(V2): Mit dem Kommutativgesetz für + in R erhält man:

$x + y = (\begin{matrix} x_{1} + y_{1} \\ ⋮ \\ x_{n} + y_{n} \end{matrix}) = (\begin{matrix} y_{1} + x_{1} \\ ⋮ \\ y_{n} + x_{n} \end{matrix}) = y + x$ .

(V3): 0 Î R ist neutral bzgl. +, also hat man:

$x + 0 = 0 + x = (\begin{matrix} 0 + x_{1} \\ ⋮ \\ 0 + x_{n} \end{matrix}) = x$ .

(V4): Mit dem oben festgesetzten Vektor -x errechnet man:

$x + (- x) = (- x) + x = (\begin{matrix} - x_{1} + x_{1} \\ ⋮ \\ - x_{n} + x_{n} \end{matrix}) = 0$ .

(V5): 1 Î R ist neutral bzgl. ·, man kann also schreiben:

$1 ċ x = (\begin{matrix} 1 ċ x_{1} \\ ⋮ \\ 1 ċ x_{n} \end{matrix}) = x$ .

(V6): Hier benutzen wir das Assoziativgesetz für · in R :

$α ċ (β ċ x) = (\begin{matrix} α (β x_{1}) \\ ⋮ \\ α (β x_{n}) \end{matrix}) = (\begin{matrix} (α β) x_{1} \\ ⋮ \\ (α β) x_{n} \end{matrix}) = (α β) ċ x$ .

(V7):  Nach dem Distributivgesetz in R gilt:

$α ċ (x + y) = (\begin{matrix} α (x_{1} + y_{1}) \\ ⋮ \\ α (x_{n} + y_{n}) \end{matrix}) = (\begin{matrix} α x_{1} + α y_{1} \\ ⋮ \\ α x_{n} + α y_{n} \end{matrix}) = (α ċ x) + (α ċ y)$ .

(V8):  Wir setzen noch einmal das Distributivgesetz ein:

$(α + β) ċ x = (\begin{matrix} (α + β) x_{1} \\ ⋮ \\ (α + β) x_{n} \end{matrix}) = (\begin{matrix} α x_{1} + β x_{1} \\ ⋮ \\ α x_{n} + β x_{n} \end{matrix}) = (α ċ x) + (β ċ x)$ .

Die auf den Koordinatenachsen des Rⁿ liegenden Vektoren spielen für die weiteren Untersuchungen eine wichtige Rolle; einige von ihnen zeichnen wir durch einen Namen aus:

Die Vektoren

e₁ :=

(\begin{matrix} 1 \\ 0 \\ ⋮ \\ 0 \end{matrix})

, e₂ :=

(\begin{matrix} 0 \\ 1 \\ ⋮ \\ 0 \end{matrix})

, .... , e_n :=

(\begin{matrix} 0 \\ ⋮ \\ 0 \\ 1 \end{matrix})

heißen die natürlichen Einheitsvektoren des Rⁿ. Ihre Koordinaten sind nur mit 0 oder 1 belegt, genauer gilt etwa für die j-te Koordinate des i-ten Einheitsvektors e_i:

(e_{i})_{j} = {\begin{array}{l} 1 &quad;, falls&quad; i = j \\ 0 &quad;, falls&quad; i &neq; j \end{array}

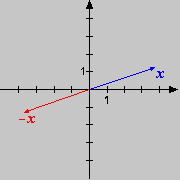
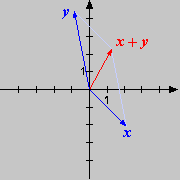
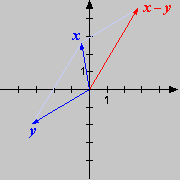
Für den R² kommen wir noch einmal auf das zu Beginn eingeführte Pfeilmodell im zurück. Hier lassen sich die Rechenoperationen mit Vektoren sehr gut geometrisch darstellen und interpretieren. Die folgenden Skizzen beschreiben die vier grundlegenden Situationen. Bei der Differenz beachte man, dass y + (x - y) = x ist.

Die Vielfachenbildung ändert die Länge, aber nicht die Richtung eines Vektors.

Der zu x inverse Vektor entsteht durch Spiegeln am Koordinatenursprung.

Die Summe x + y ist die Hauptdiagonale des von x und y aufgespannten Parallelogramms.

Die Differenz x - y liegt parallel zur Nebendiagonalen des von x und y aufgespannten Parallelogramms.

Zentrales Beispiel (2): Für eine beliebige Menge A bezeichne

F (A) := { f : A ® R }

die Menge aller reellwertigen Funktionen auf A. Setzt man für f, g Î F (A) und a Î R :

f + g (x) := f(x) + g(x), x Î A

a·f (x) := a( f(x)), x Î A

so ist (F (A), + , · ) ein Vektorraum.

Dabei ist

Die Nullfunktion 0 der Nullvektor.
Die Funktion -f der zu f inverse Vektor.
f - g ist die Differenz zweier Funktionen.

Beweis: Die Vektorraumaxiome (V1) bis (V8) sind jetzt bestimmte Rechenregeln für Funktionen. Als solche sind sie bereits alle in Kapitel 4.4. bewiesen!

Mit den Räumen F (A) steht uns, analog zu den Räumen Rⁿ, eine ganze Gruppe von Vektorräumen zur Verfügung. Konkrete Beispiele sind etwa F (R ), oder allgemeiner F (R ⁿ), F (R ^>⁰), aber auch F (N ) = {(a_n) | n Î N }, der Vektorraum aller Folgen.

Im nächsten Abschnitt werden wir weitere Vektorräume erhalten, indem wir gewisse Teilsysteme von F (A) betrachten.

Die acht Vektorraumaxiome stellen einen recht umfangreichen Katalog von Bedingungen dar; es ist daher zu erwarten, dass Vektorräume eine reiche algebraische Struktur haben.

Die folgenden Rechenregeln lassen sich direkt aus den Axiomen ableiten.

Bemerkung: Es sei (V, + , · ) ein Vektorraum, dann gilt für v,w Î V, a Î R :

a·0 = 0

0·v = 0

a·v = 0    Û   a = 0    Ú    v = 0

(-1)·v = -v

a·(-v) = -a·v = (-a)·v

a·(v - w) = a·v - a·w

$\frac{v + w}{α} = \frac{v}{α} + \frac{w}{α}$   , für a ¹ 0

$\frac{v - w}{α} = \frac{v}{α} - \frac{w}{α}$   , für a ¹ 0

Ist a ¹ 0, so besitzt jede Gleichung der Form a·x + v = w genau eine Lösung:

a·x + v = w   Û   x = $\frac{w - v}{α}$ .

Beweis:

Zu 1.: Da 0 + 0 = 0, folgt aus dem Distributivgesetz (V7):

a·0 = a·(0 + 0) = a·0 + a·0

Þ     0 = a·0 - a·0 = (a·0 + a·0) - a·0 = a·0.

Zu 2.: Ähnlich zu 1. argumentiert man hier mit dem zweiten Distributivgesetz (V8):

0·v = (0 + 0)·v = 0·v + 0·v

Þ     0 = 0·v - 0·v = (0·v + 0·v) - 0·v = 0·v.

Zu 3.: Ü" steht in 1. und 2. Für die Richtung "Þ" sei a·v = 0 gegeben. Falls a ¹ 0, hat man: v = $\frac{1}{α}$ (a·v) = 0.

Zu 4.: Wir benutzen (V5) und (V8):

(-1)·v + v = (-1)·v + 1·v = (-1 +1)·v = 0·v = 0

Þ     (-1)·v = (-1)·v + (v - v) = ((-1)·v + v) - v = - v.

Zu 5.: Aus dem bisher Gezeigten ergibt sich mit (V6):

a·(-v) = a·((-1)·v) = (a·(-1))·v

= (-a)·v

= (-1a)·v = (-1)·(a·v) = -a·v.

Zu 6.:

a·(v - w)   = a·(v + (- w))

= a·v + a·(- w)

= a·v + (-a·w)

= a·v - a·w.

Zu 7.:  Dieses Distributivgesetz läßt sich auf (V7) zurückführen:

$\frac{v + w}{α} = \frac{1}{α} (v + w) = \frac{1}{α} v + \frac{1}{α} w = \frac{v}{α} + \frac{w}{α}$ .

Zu 8.:  Analog zu 6. erhält man diese Behauptung aus 5.

Zu 9.:  Die Äquivalenz ergibt sich wie gewohnt durch Auflösen nach x.

Wir beschließen den einführenden Abschnitt mit einem weiteren Beispiel und stellen den kleinsten Vektorraum, den sog. Nullraum vor.

Bemerkung und Definition: Es sei 0 ein beliebiges Element. Durch die Festsetzung

0 + 0 := 0
a· 0 := 0

werden zwei Rechenoperationen

+ : {0} ´ {0} ® {0}
· : R ´ {0} ® {0}

erklärt, die trivialerweise die Axiome (V1) bis (V8) erfüllen. Der Vektorraum ({0}, + , · ) heißt der Nullraum. Er ist einelementig und überdies der einzige (reelle!) Vektorraum mit endlichen vielen Elementen:

Ist (V, + , · ) nicht der Nullraum, so gibt es eine injektive Abbildung von N nach V.

Beweis: Da V nicht der Nullraum ist, gibt es in V einen Vektor v ¹ 0. Durch die Festsetzung f(n) := nv ist eine Funktion

f : N ® V

gegeben. Wir weisen f als injektiv nach: Sei dazu nv = mv, also (n - m)v = 0. Da v ¹ 0 ist, muss n - m = 0 sein, d.h. aber: n = m.

9.2.

- - - - - Diese Seite braucht webEQ! Klicken Sie auf das Logo. - - - - -
9.1. Vektorräume und Vektoren